高階導數十個常用公式

高階導數是微積分中的一個重要概念，它描述了函數在某一點的切線斜率的變化率。以下是一些常用的高階導數公式：

1. 冪函數的高階導數：

\[ (x^n)^{(n)} = n! \cdot x^{n-n} = n! \]

其中 \( n! \) 表示 \( n \) 的階乘，即 \( n! = n \times (n-1) \times \ldots \times 2 \times 1 \)。

2. 三角函數的高階導數：

- \( \sin(x) \) 的高階導數：

\[ \sin^{(n)}(x) = \cos((2k-n)x) \text{ 當 } n = 2k \]

\[ \sin^{(n)}(x) = -\sin((2k+1-n)x) \text{ 當 } n = 2k+1 \]

- \( \cos(x) \) 的高階導數：

\[ \cos^{(n)}(x) = -\sin((2k-n)x) \text{ 當 } n = 2k \]

\[ \cos^{(n)}(x) = \sin((2k+1-n)x) \text{ 當 } n = 2k+1 \]

3. 指數函數的高階導數：

\[ (e^x)^{(n)} = e^x \]

指數函數的所有階導數都是它本身。

4. 對數函數的高階導數：

\[ (\ln(x))^{(n)} = (-1)^{n-1} \frac{(1-x)^{n-1}}{x^n} \text{ 當 } x > 0 \]

5. 雙曲函數的高階導數：

- \( \sinh(x) \) 的高階導數：

\[ \sinh^{(n)}(x) = \cosh((2k-n)x) \text{ 當 } n = 2k \]

\[ \sinh^{(n)}(x) = \sinh((2k+1-n)x) \text{ 當 } n = 2k+1 \]

- \( \cosh(x) \) 的高階導數：

\[ \cosh^{(n)}(x) = \sinh((2k-n)x) \text{ 當 } n = 2k \]

\[ \cosh^{(n)}(x) = \cosh((2k+1-n)x) \text{ 當 } n = 2k+1 \]

6. 乘積的高階導數（萊布尼茨公式）：

\[ (fg)^{(n)} = \sum_{k=0}^{n} (f^{(k)}g^{(n-k)}) \]

其中 \( f \) 和 \( g \) 是可導函數。

7. 商的高階導數（商規則的推廣）：

\[ \left(\frac{f}{g}\right)^{(n)} = \frac{P_n(f, g)}{g^{n+1}} \]

其中 \( P_n(f, g) \) 是 \( f \) 和 \( g \) 及其導數的多項式。

8. 鏈式法則的高階導數：

\[ (f(g(x)))^{(n)} = \sum_{k=1}^{n} f^{(k)}(g(x)) \cdot g^{(n-k)}(x) \]

其中 \( f \) 和 \( g \) 是可導函數。

這些公式是高階導數計算的基礎，可以幫助解決更復雜的微積分問題。

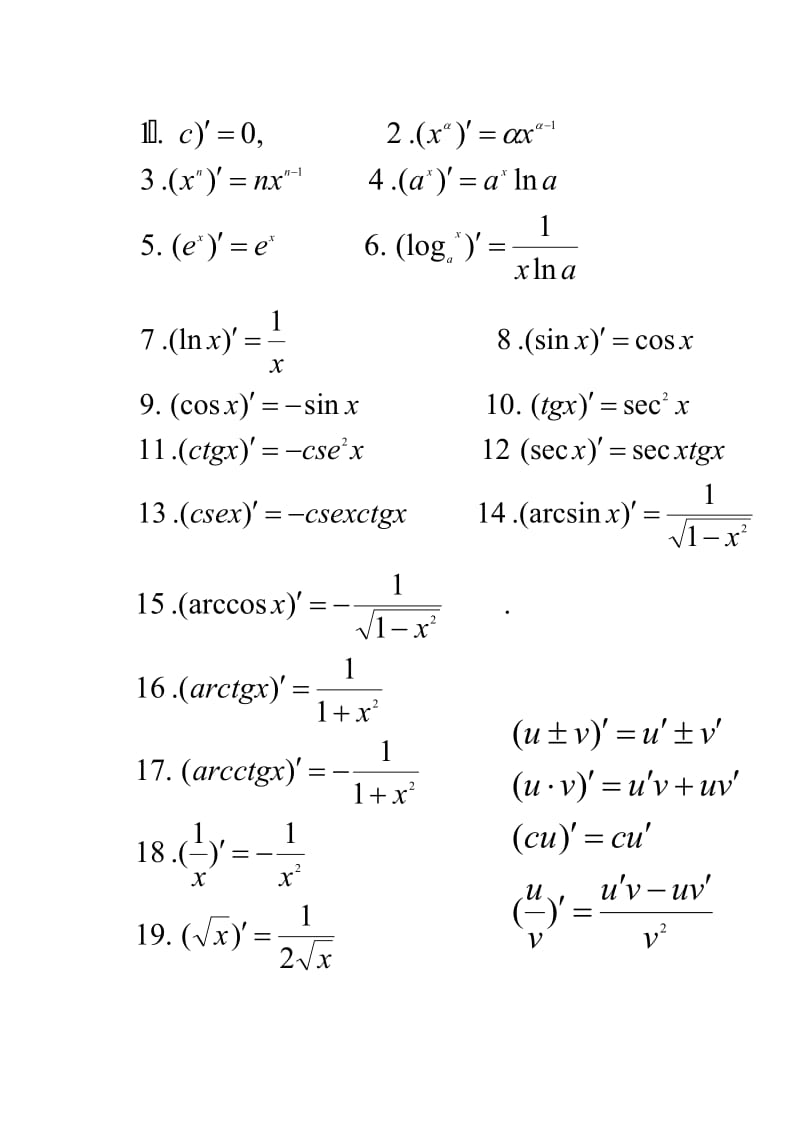
6種常見函數的高階導數

在數學中，高階導數是指函數的導數的導數，也就是多次求導。以下是六種常見函數及其高階導數的一般形式：

1. 常數函數 \( f(x) = c \)（其中 \( c \) 是常數）

- 任何階導數都是 0。

2. 冪函數 \( f(x) = x^n \)（其中 \( n \) 是實數）

- 一階導數：\( f'(x) = nx^{n-1} \)

- 高階導數：\( f^{(n)}(x) = n(n-1)(n-2)...(n-k+1)x^{n-k} \)，其中 \( k \) 是導數的階數。

3. 指數函數 \( f(x) = e^x \)

- 所有階導數：\( f^{(n)}(x) = e^x \)

4. 對數函數 \( f(x) = \ln(x) \)（自然對數）

- 一階導數：\( f'(x) = 1/x \)

- 高階導數：\( f^{(n)}(x) = (-1)^{n-1} \frac{(n-1)!}{x^n} \)

5. 三角函數 \( \sin(x) \) 和 \( \cos(x) \)

- \( \sin(x) \) 的一階導數：\( \cos(x) \)

- \( \cos(x) \) 的一階導數：\( -\sin(x) \)

- 高階導數：\( \sin(x) \) 和 \( \cos(x) \) 的高階導數會交替出現，每4次導數后重復。

6. 雙曲正弦和雙曲余弦函數 \( \sinh(x) \) 和 \( \cosh(x) \)

- \( \sinh(x) \) 的一階導數：\( \cosh(x) \)

- \( \cosh(x) \) 的一階導數：\( \sinh(x) \)

- 高階導數：\( \sinh(x) \) 和 \( \cosh(x) \) 的高階導數會交替出現，每4次導數后重復。

這些是基本函數的高階導數的一般形式。對于更復雜的函數，高階導數可以通過復合函數的導數規則來計算。

n階導數公式大全

在數學中，n階導數是指函數的導數連續求n次的結果。以下是一些基本函數的n階導數公式：

1. 常數函數 \( f(x) = c \)：

- \( f'(x) = 0 \)（一階導數）

- 對于所有 \( n > 1 \)，\( f^{(n)}(x) = 0 \)

2. 冪函數 \( f(x) = x^n \)（\( n \) 是實數）：

- \( f^{(n)}(x) = n! \cdot x^{n-n} = n! \) 當 \( x = 0 \) 時，\( n > 1 \) 的情況除外。

3. 指數函數 \( f(x) = a^x \)（\( a > 0, a \neq 1 \)）：

- \( f^{(n)}(x) = a^x \ln(a)^n \)

4. 對數函數 \( f(x) = \ln(x) \)（\( x > 0 \)）：

- \( f^{(n)}(x) = (-1)^{n-1} \frac{(n-1)!}{x^n} \)

5. 三角函數：

- \( \sin(x) \) 的n階導數：\( f^{(n)}(x) = \sin(x + n\pi/2) \) 或 \( (-1)^{k} \cos(x) \) 當 \( n = 2k+1 \)，\( (-1)^{k} \sin(x) \) 當 \( n = 2k \)

- \( \cos(x) \) 的n階導數：\( f^{(n)}(x) = \cos(x - n\pi/2) \) 或 \( (-1)^{k} \sin(x) \) 當 \( n = 2k+1 \)，\( (-1)^{k+1} \cos(x) \) 當 \( n = 2k \)

6. 反三角函數：

- \( \arcsin(x) \) 的n階導數：\( f^{(n)}(x) = \frac{P_n(x)}{1-x^2} \)，其中 \( P_n(x) \) 是 \( x \) 的多項式。

- \( \arccos(x) \) 的n階導數：\( f^{(n)}(x) = (-1)^{n+1} \frac{Q_n(x)}{1-x^2} \)，其中 \( Q_n(x) \) 是 \( x \) 的多項式。

7. 正割函數 \( \sec(x) \) 和余割函數 \( \csc(x) \)：

- \( \sec(x) \) 的n階導數：\( f^{(n)}(x) = \sec(x)\tan(x) \cdot f^{(n-1)}(\tan(x)) \)

- \( \csc(x) \) 的n階導數：\( f^{(n)}(x) = -\csc(x)\cot(x) \cdot f^{(n-1)}(\cot(x)) \)

8. 雙曲正弦和余弦函數 \( \sinh(x) \) 和 \( \cosh(x) \)：

- \( \sinh(x) \) 的n階導數：\( f^{(n)}(x) = \cosh(x) \) 當 \( n \) 是奇數，\( \sinh(x) \) 當 \( n \) 是偶數。

- \( \cosh(x) \) 的n階導數：\( f^{(n)}(x) = \sinh(x) \) 當 \( n \) 是奇數，\( \cosh(x) \) 當 \( n \) 是偶數。

這些是一些基本函數的n階導數公式。對于更復雜的函數，n階導數的計算可能需要使用導數的運算法則，如乘積法則、商法則、鏈式法則等。如果你需要更具體的函數的n階導數公式，可以提供具體的函數形式，我可以幫助你計算。